课程 31 - 图形间的连接关系

在课程 23 - 思维导图中，我们仅关注了节点和边的布局算法，并没有深入交互，例如移动节点时绑定的边也要跟着移动。同样在课程 25 - 绘制箭头中，直线和箭头的属性中也不包含绑定信息，这节课我们将补全这一点。

数据结构

Excalidraw 中的线性元素

Excalidraw 中，连接线（如箭头）在数据模型中用 ExcalidrawLinearElement 表示，该类型增加了连接相关字段：

export declare type PointBinding = {
    elementId: ExcalidrawBindableElement['id'];
    focus: number;
    gap: number;
};
export declare type ExcalidrawLinearElement = _ExcalidrawElementBase &
    Readonly<{
        type: 'line' | 'arrow';
        points: readonly Point[];
        lastCommittedPoint: Point | null;
        startBinding: PointBinding | null;
        endBinding: PointBinding | null;
        startArrowhead: Arrowhead | null;
        endArrowhead: Arrowhead | null;
    }>;

如上所示，每条箭头具有可选的 startBinding 和 endBinding 字段，它们与 points 处在不同的语义层级，前者为语义约束，而后者 points 为几何表示，当两者同时存在时，points 需要被重新计算。以及起止箭头样式（startArrowhead/endArrowhead）。PointBinding 中的 elementId 指向被连接的图形（可绑定元素，如矩形、椭圆、文本、图片等），focus 和 gap 则用于定位连接点（一个浮点索引和偏移距离）。例如，下面是一个箭头元素在 JSON 中的示例：

{
  "type": "arrow",
  // ... 省略其它属性 ...
  "startBinding": {
    "elementId": "xw25sQBsbd2mecyjTrYHA",
    "focus": -0.0227,
    "gap": 15.6812
  },
  "endBinding": null,
  "points": [[0,0],[0,109]],
  "startArrowhead": null,
  "endArrowhead": null
}

在该例中，箭头的 startBinding 指向 ID 为 "xw25sQBsbd2mecyjTrYHA" 的图形，focus 和 gap 定义了从该图形边界出发的连接位置。

同时，每个被绑定的图形（例如矩形或椭圆）的基本数据结构里有一个 boundElements 列表，用于记录所有连接到它的箭头或文本元素。该字段类型通常为 { id: ExcalidrawLinearElement["id"]; type: "arrow"|"text"; }[] | null。也就是说，箭头与图形之间的连接是双向维护的：箭头记录自己绑定的目标元素 ID，目标元素记录指向它的箭头 ID。

tldraw 中的绑定

在 tldraw 中，“连线”本身也是一种形状（默认是箭头形状），其连接关系通过绑定（Binding）对象来表示。每个绑定记录在存储中单独存在，表示两个形状间的关联。对于箭头连接，使用 TLArrowBinding 类型，它是 TLBaseBinding<'arrow',TLArrowBindingProps> 的特化。一个典型的箭头绑定记录示例如下：

{
  id: 'binding:abc123',
  typeName: 'binding',
  type: 'arrow',           // 绑定类型为箭头
  fromId: 'shape:arrow1',  // 箭头形状的ID（箭头形状出发端）
  toId:   'shape:rect1',   // 目标形状的ID（箭头指向的形状）
  props: {
    terminal: 'end',       // 绑定到箭头的哪一端（start 或 end）
    normalizedAnchor: { x: 0.5, y: 0.5 }, // 目标形状上的标准化锚点
    isExact: false,        // 箭头是否进入目标形状内部
    isPrecise: true,       // 是否精确使用锚点，否则使用形状中心
    snap: 'edge',          // 吸附模式（如贴边等）
  },
  meta: {}
}

这里 fromId/toId 字段以形状 ID 的方式关联箭头与目标，props 中存储了连接细节（如锚点、对齐选项等）

antv/g6

连接关系是逻辑的，不是几何的，通过 type 和连线路由算法计算路径：

interface EdgeConfig {
    id?: string;
    source: string; // 源节点 ID
    target: string; // 目标节点 ID

    sourceAnchor?: number; // 源节点锚点索引
    targetAnchor?: number; // 目标节点锚点索引

    type?: string; // line / polyline / cubic / loop ...
    style?: ShapeStyle;
}

在节点上声明锚点，坐标是归一化的：

anchorPoints: [
    [0.5, 0], // top
    [1, 0.5], // right
    [0.5, 1], // bottom
    [0, 0.5], // left
];

在边上使用锚点索引，和 tldraw 的 normalizedAnchor 非常像，但 G6 把锚点定义权放在节点上

{
    source: 'nodeA',
    target: 'nodeB',
    sourceAnchor: 1,
    targetAnchor: 3,
}

mxGraph

mxGraph 有完整的连接约束系统，定义在节点图形上，表示允许连接的点：

class mxConnectionConstraint {
    point: mxPoint | null; // (0.5, 0) = 上中 (1, 0.5) = 右中
    perimeter: boolean; // 表示沿形状边界投射
}

JSON Canvas Spec

Obsidian 开放了 JSON Canvas Spec，结构上和 antv/g6 很类似，在顶层存储了节点和边数组：

json

{
    "nodes": [],
    "edges": []
}

边的结构如下，不包含几何信息，只有逻辑上的连接关系：

json

{
    "id": "f67890123456789a",
    "fromNode": "6f0ad84f44ce9c17",
    "toNode": "a1b2c3d4e5f67890"
}

我们的设计

在 Schema 上我们更多参考 mxGraph 的设计。逻辑关系在边上通过 fromId 和 toId 体现，此时就不需要 x1/y1 之类的几何信息。一个连接了 rect-1 和 rect-2 的箭头声明如下：

const edge1 = {
    id: 'line-1',
    type: 'line',
    fromId: 'rect-1',
    toId: 'rect-2',
    stroke: 'black',
    strokeWidth: 10,
    markerEnd: 'line',
};

同时约束关系体现在节点上，类似 mxConnectionConstraint：

interface ConstraintAttributes {
    /**
     * Normalized point, relative to bounding box top-left.
     */
    point: [number, number];
    /**
     * Use perimeter.
     */
    perimeter: boolean;
    name?: string;
    dx?: number;
    dy?: number;
}

类似课程 18 - 定义父子组件，我们可以实现双向绑定关系：

class Binding {
    @field.ref declare from: Entity;
    @field.ref declare to: Entity;
}

class Binded {
    @field.backrefs(Binding, 'from') declare fromBindings: Entity[];
    @field.backrefs(Binding, 'to') declare toBindings: Entity[];
}

自动更新

当连接的图形位置发生变化时，需要重新计算绑定边的路径。我们可以查询所有持有 Binded 组件的图形，监听它们的包围盒变化，此时更新绑定的边：

class RenderBindings extends System {
    private readonly boundeds = this.query(
        (q) => q.with(Binded).changed.with(ComputedBounds).trackWrites,
    );

    execute() {
        const bindingsToUpdate = new Set<Entity>();
        this.boundeds.changed.forEach((entity) => {
            const { fromBindings, toBindings } = entity.read(Binded);
            [...fromBindings, ...toBindings].forEach((binding) => {
                bindingsToUpdate.add(binding);
            });
        });
        // 重新计算绑定边的路径并渲染
    }
}

在下面的例子中，你可以尝试拖动节点，边会重新计算路径并重绘：

目前边的起点和终点都是被连接图形的包围盒中心，和 tldraw 中 isPrecise 等于 false 时效果一致，表示不精确绑定。而大多数情况下，我们希望箭头不穿过所连接的图形，而是优雅地停靠在图形边缘。

边界算法

对于图形的边界，drawio 提供了 perimeter 属性，改变它会导致连线，详见：Change the shape perimeter

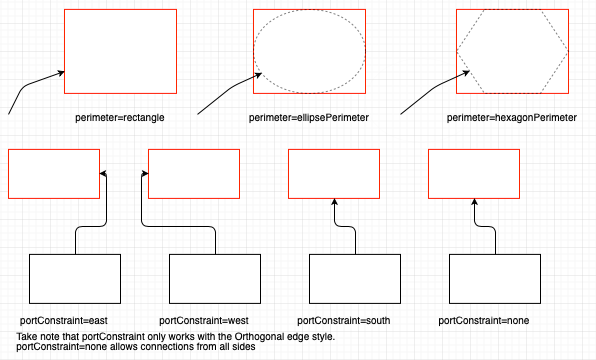
// 注意一般 next 传入的是“对方中心点”，orthogonal 通常选 false
var pointA = graph.view.getPerimeterPoint(stateA, centerB, false, 0);
var pointB = graph.view.getPerimeterPoint(stateB, centerA, false, 0);

矩形边界算法

矩形的边界算法是最常用的。以下实现中 vertex 为源节点，next 为目标节点的包围盒中心。首先从源节点和目标节点包围盒的中心做一条连线，然后判断目标点离源节点包围盒的哪条边更近，包围盒的两条对角线将平面划分成了四个区域，左侧边界的范围是 $[- π + t, π - t]$ 之外的区域（即代码中 alpha < -pi + t || alpha > pi - t 的判断）：

function rectanglePerimeter(
    vertex: SerializedNode,
    next: IPointData,
    orthogonal: boolean,
): IPointData {
    const { x, y, width, height } = vertex;
    const cx = x + width / 2; // 源节点中心
    const cy = y + height / 2;
    const dx = next.x - cx;
    const dy = next.y - cy;
    const alpha = Math.atan2(dy, dx); // 源节点中心到目标节点中心连线的斜率
    const p: IPointData = { x: 0, y: 0 };
    const pi = Math.PI;
    const pi2 = Math.PI / 2;
    const beta = pi2 - alpha;
    const t = Math.atan2(height, width); // 对角线划分了四个区域
    if (alpha < -pi + t || alpha > pi - t) {
        // 与左侧边缘相交
        p.x = x;
        p.y = cy - (width * Math.tan(alpha)) / 2; // 计算交点
    }
    // 省略其他三条边
    return p;
}

最后计算连线与该边的交点作为最终连线的出发点。例如我们确定了连线会经过“左侧边”时：

确定 $x$ 坐标：既然是左边缘，交点的 $x$ 坐标必然等于矩形的左边界值 vertex.x。
计算 $y$ 偏移量：
1. 从中心到左边缘的水平距离是 width / 2。
2. 利用正切公式： $\tan (α) = \frac{Δ y}{Δ x}$ 。
3. 在左侧， $Δ x = - (width / 2)$ 。
4. 所以垂直偏移量 $Δ y = Δ x \cdot \tan (α) = - \frac{width}{2} \cdot \tan (α)$ 。
最终坐标： p.y = cy + Δy，即代码中的 cy - (width * Math.tan(alpha)) / 2。

draw.io 还提供了另一个选项 orthogonal，表示计算的线需要正交对齐（即与 x 或 y 轴对齐），线只考虑水平或垂直延伸。此时就不能使用对方的中心点作为参考了：

if (orthogonal) {
    if (next.x >= x && next.x <= x + width) {
        p.x = next.x;
    } else if (next.y >= y && next.y <= y + height) {
        p.y = next.y;
    }
    if (next.x < x) {
        p.x = x;
    } else if (next.x > x + width) {
        p.x = x + width;
    }
    if (next.y < y) {
        p.y = y;
    } else if (next.y > y + height) {
        p.y = y + height;
    }
}

椭圆边界算法

对于椭圆节点，需要计算直线和它的交点：

const d = dy / dx;
const h = cy - d * cx;
const e = a * a * d * d + b * b;
const f = -2 * cx * e;
const g = a * a * d * d * cx * cx + b * b * cx * cx - a * a * b * b;
const det = Math.sqrt(f * f - 4 * e * g);

const xout1 = (-f + det) / (2 * e);
const xout2 = (-f - det) / (2 * e);
const yout1 = d * xout1 + h;
const yout2 = d * xout2 + h;
const dist1 = Math.sqrt(Math.pow(xout1 - px, 2) + Math.pow(yout1 - py, 2));
const dist2 = Math.sqrt(Math.pow(xout2 - px, 2) + Math.pow(yout2 - py, 2));

let xout = 0;
let yout = 0;
if (dist1 < dist2) {
    xout = xout1;
    yout = yout1;
} else {
    xout = xout2;
    yout = yout2;
}
return { x: xout, y: yout };

连线经过中心 $(c x, c y)$ ，其方程为 $y = d \cdot x + h$ ：

斜率 $d = \frac{d y}{d x}$
截距 $h = c y - d \cdot c x$

将直线方程代入椭圆标准方程：

\frac{(x - c x)^{2}}{a^{2}} + \frac{(d \cdot x + h - c y)^{2}}{b^{2}} = 1

展开并整理成关于 $x$ 的一元二次方程形式 $e x^{2} + f x + g = 0$ 。代码中的 e, f, g 分别对应：

$e$ : 二次项系数
$f$ : 一次项系数
$g$ : 常数项

求根公式：使用判别式 $d e t = \sqrt{f^{2} - 4 e g}$ 算出两个交点 $x o u t 1$ 和 $x o u t 2$ 。两点选一：射线穿过椭圆会产生两个交点（一前一后）。代码通过计算两个交点到目标点 next 的距离（dist1 和 dist2），选择距离最近的那个点。

定义约束

至此，我们实现了在边上仅通过 fromId 和 toId 表达逻辑连接关系的实现。边和节点的连接点是浮动的，在 mxGraph 中称作 FloatingTerminalPoint。但有时我们希望边从节点的固定位置离开、从被连接图形的固定位置进入，在 mxGraph 称作 FixedTerminalPoint，此时就需要通过约束定义，分成节点和边两部分。

节点约束

节点约束表示允许你从哪些位置、以什么规则连线，它不是一个“点”，而是一个规则对象，在 mxGraph 中定义如下：

class mxConnectionConstraint {
    point: mxPoint | null; // 归一化坐标 (0~1)
    perimeter: boolean; // 是否投射到边界
    name?: string; // 可选，端口名
}

在配套的 draw.io 的编辑器中我们能看到图形上许多“蓝色连接点”，它们就是通过重载图形上的约束定义的：

mxRectangleShape.prototype.getConstraints = function (style) {
    return [
        new mxConnectionConstraint(new mxPoint(0.5, 0), true), // top
        new mxConnectionConstraint(new mxPoint(1, 0.5), true), // right
        new mxConnectionConstraint(new mxPoint(0.5, 1), true), // bottom
        new mxConnectionConstraint(new mxPoint(0, 0.5), true), // left
    ];
};

我们的约束定义如下，在节点上可以声明一组约束：

export interface ConstraintAttributes {
    x?: number;
    y?: number;
    perimeter?: boolean;
    dx?: number;
    dy?: number;
}

export interface BindedAttributes {
    constraints: ConstraintAttributes[];
}

获取候选约束，选择最近的约束，将约束转为几何点。如果需要投射到边界，就进入上一节介绍过的边界算法计算逻辑。

边约束

在边上也需要定义从节点的哪个锚点上离开或进入，在交互操作上对应将边的端点拖拽到节点的锚点上，此时 entryX/entryY 就需要拷贝锚点约束的 x/y 字段：

interface BindingAttributes {
    fromId: string;
    toId: string;
    orthogonal: boolean;
    exitX: number; 
    exitY: number; 
    exitPerimeter: boolean; 
    exitDx: number; 
    exitDy: number; 
    entryX: number; 
    entryY: number; 
    entryPerimeter: boolean; 
    entryDx: number; 
    entryDy: number; 
}

在下面的例子中，我们分别在灰色和绿色矩形上各定义了一个锚点 [1, 0] 和 [0, 1]

[WIP] 路由规则

mxGraph 使用 EdgeStyle 函数来实现路由规则，这些函数负责：

自动选择出口方向
插入拐点（Waypoints）
避开节点包围盒
计算正交/直角路径

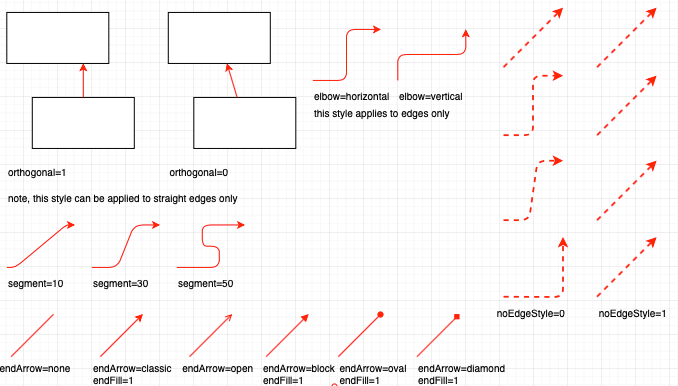
在编辑器初始化时注册这些函数：

mxStyleRegistry.putValue(mxConstants.EDGESTYLE_ORTHOGONAL, mxEdgeStyle.OrthConnector);

OrthConnector

OrthConnector 是最常见的路由算法：

确定源和目标的【出口/入口方向】
根据方向组合查找【预定义路由模式】
应用路由模式生成【拐点序列】
处理【避障】和【优化】

┌──────┐        ┌──────┐
│ Node │ ─┐     │ Node │
└──────┘  └────▶└──────┘

[WIP] 导出 SVG

在导出时，就不能只保存几何信息了，还需要将逻辑关系也一并持久化。

html

<line x1="0" y1="0" data-binding="" />

[WIP] 编辑器

高亮锚点

选中节点时，展示可用的锚点，从锚点可以发起连线。
选中边时，拖拽时高亮可停靠的锚点。

课程 31 - 图形间的连接关系 ​

数据结构 ​

Excalidraw 中的线性元素 ​

tldraw 中的绑定 ​

antv/g6 ​

mxGraph ​

JSON Canvas Spec ​

我们的设计 ​

自动更新 ​

边界算法 ​

矩形边界算法 ​

椭圆边界算法 ​

定义约束 ​

节点约束 ​

边约束 ​

[WIP] 路由规则 ​

OrthConnector ​

[WIP] 导出 SVG ​

[WIP] 编辑器 ​

高亮锚点 ​